A spring-mass system, kl and m, has a natural frequency of fl. If a second spring k2 is added in series with the first spring, the natural frequency is lowered to 1/2 fl. Determine k2 in terms of kl.
__________________________________________________________________________________
 |
| An unknown mass of m kg attached to the end of an unknown spring k has a natural frequency
of 94 cpm. When a 0.453 kg mass is added to m, the natural frequency is lowered to 76.7 cpm.
Determine the unknown mass m and the spring constant kN/m |
__________________________________________________________________________________
 |
| A cylinder of mass m and mass moment of inertia Jo is
free to roll without slipping, but is restrained by the
spring k, as shown in the following figure. Determine
the natural frequency of oscillation. |
 |
| A cylinder of mass m and mass moment of inertia Jo is free to roll without slipping, but is restrained by the spring k, as shown in the following figure. Determine the natural frequency of oscillation. |
|
__________________________________________________________________________________
 |
For a simple pendulum shown in the following figure, derive the
equation of motion applying newton’s second law, the energy method
and the momentum method assuming θ is small angle.
|
__________________________________________________________________________________
 |
Determine the effective mass at point n and its natural frequency for the system shown in the
following figure:
__________________________________________________________________________________
|
 |
Determine the effective rotational stiffness of the
shaft in the following figure and calculate its
natural period.
|
 |
Determine the effective rotational stiffness of the shaft in the following figure and calculate its natural period.
__________________________________________________________________________________
|
 |
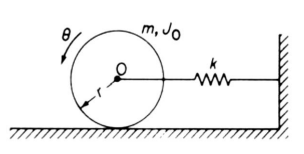
| Determine the kinetic energy of the system shown in the following figure in terms of 𝑥̇.
Determine the stiffness at mo, and write the expression for the natural frequency |
